Primitive per la grafica 2D

Nella geometria, una primitiva è la più semplice delle figure geometriche. Tutte le figure più complesse si costruiscono combinando più primitive.

Nella moderna computer grafica, le primitive grafiche sono le funzioni che realizzano le figure geometriche più elementari, come punti, segmenti, archi e poligoni, e saranno spiegate in questo capitolo. Per le primitive che realizzano figure più complesse, come le curve spline e le curve di Bézier si rimanda alle specifiche tecniche e agli esempi ufficiali.

Alcuni poligoni ed alcune curve sono considerati primitive, anche se possono essere realizzati combinando altre primitive, ad esempio i segmenti possono essere realizzati con più punti ed i poligoni con più segmenti, ma le primitive grafiche facilitano il lavoro del programmatore nella creazione di queste figure. Inseriremo anche funzione per la creazione dell’area da disegno tra le primitive grafiche, anche se non realizza alcuna figura geometrica.

Dal precedente capitolo abbiamo imparato che ogni funzione (e le primitive sono funzioni) ha una firma composta dal nome e dalla lista di parametri formali. La lista di parametri formali è riportata tra parentesi tonde, ogni parametro può essere obbligatorio o facoltativo. Di seguito le varie primitive saranno descritte indicando la firma.

Di seguito saranno descritte quindi le varie figure geometriche e le funzioni che le realizzano, indicando la firma e descrivendo gli argomenti necessari.

Creazione dell’area da disegno

L’area da disegno è la tavola sulla quale disegnare ed è caratterizzata da una larghezza ed un’altezza. La funzione progettata allo scopo è createCanvas, la cui firma è la seguente:

Syntax: createCanvas(w, h)

Parameters:
    w    Number: width of the canvas
    h    Number: height of the canvas

I parametri formali sono w ed h e rappresentano la larghezza e l’altezza dell’area da disegno.

Per creare un’area da disegno di larghezza 600 ed altezza 400 punti, sostituiamo:

• al parametro formale w (che indica la larghezza dell’area da disegno) il valore 600;
• al parametro formale h (che indica l’altezza dell’area da disegno) il valore 400.

La funzione viene quindi invocata nel seguente modo:

createCanvas(600, 400);

Disegno di un punto

Il punto è un’entità geometrica senza dimensioni, ovvero non ha estensione, cioè non ha larghezza, altezza o profondità, ma ha una posizione (nel piano, nello spazio, dipende dal sistema di coordinate). Tipicamente al punto viene associato un nome letterale (ad esempio P, Q, R).

Nella computer grafica un punto deve poter essere disegnato sullo schermo, quinti ha una dimensione che è di un pixel dello schermo, ed ha un colore.

La posizione di un punto è indicata da due coordinate del piano, l’ascissa e l’ordinata (o tre coordinate nel caso di uno spazio a tre dimensioni).

La primitiva grafica che permette di disegnare un punto in una certa posizione dell’area da disegno è point, la cui firma è la seguente:

Syntax: point(x, y, [z])

Parameters:
    x   Number: the x-coordinate
    y   Number: the y-coordinate
    z   Number: the z-coordinate (for WebGL mode) (Optional)

I parametri formali sono x, y e z e rappresentano le coordinate del punto. I primi due parametri sono obbligatori e rappresentano le coordinate in un piano, il terzo parametro è tra parentesi quadre, quindi è opzionale, e lo si utilizza per indicare una terza coordinata in un sistema a tre dimensioni (non più un piano, ma uno spazio). Questo terzo parametro si usa solo quando si attiva la modalità WebGL, che non sarà trattata in questo capitolo.

Per creare un punto alle coordinate (20, 20), sostituiamo:

• al parametro formale x (che indica la coordinata X) il valore 20;
• al parametro formale y (che indica la coordinata Y) il valore 20.

La funzione viene quindi invocata nel seguente modo:

point(20, 20);

Il risultato è visualizzato nell’immagine seguente:

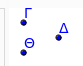
Disegno di un segmento rettilineo

Geometricamente una linea è un insieme illimitato di punti che si estendono in una direzione. Non ha larghezza o spessore. Può essere retta, curva, inclinata o ondulata, a seconda delle sue proprietà specifiche. Dal punto di vista matematico, una linea è descritta da un’equazione, ad esempio un’equazione lineare genera una retta, un’equazione quadratica produce una curva.

Un segmento è una porzione di linea (retta, curva, ondulata, l’importante è che sia continua) che unisce due estremi, indicati da un punto iniziale ed un punto finale.

Nella computer grafica per linea si intende un segmento rettilineo, ovvero una porzione di retta che unisce due estremi, indicati da un punto iniziale ed un punto finale.

Due segmenti si dicono consecutivi o adiacenti se condividono esclusivamente un estremo comune, cioè se il punto di fine di un segmento coincide con il punto di inizio dell’altro segmento. La caratteristica dei segmenti adiacenti è che possono avere diverse lunghezze e angolature, ma sono collocati uno dietro l’altro in modo sequenziale.

Due segmenti rettilinei si dicono adiacenti se hanno un estremo in comune ed appartengono alla stessa retta, di conseguenza hanno la stessa angolatura.

Due segmenti si dicono perpendicolari se si incontrano formando un angolo retto (90 gradi) tra di loro. Si dicono paralleli se mantengono sempre la stessa distanza tra di loro lungo tutta la loro lunghezza.

La primitiva grafica che permette di disegnare un segmento rettilineo delimitato da due punti) è line, la cui firma è la seguente:

Syntax: line(x1, y1, x2, y2)

Parameters:
    x1    Number: the x-coordinate of the first point
    y1    Number: the y-coordinate of the first point
    x2    Number: the x-coordinate of the second point
    y2    Number: the y-coordinate of the second point

I parametri formali x1 ed y1 rappresentano le coordinate del punto da cui parte la linea ed i parametri formali x2 ed y2 rappresentano le coordinate del punto in cui la linea termina.

Per creare una linea che parte dal punto alle coordinate (80, 20) e termina al punto alle coordinate (120, 40), sostituiamo:

• al parametro formale x1 (che indica la coordinata X del punto di partenza) il valore 80;
• al parametro formale y1 (che indica la coordinata Y del punto di partenza) il valore 20;
• al parametro formale x2 (che indica la coordinata X del punto di arrivo) il valore 120;
• al parametro formale y2 (che indica la coordinata Y del punto di arrivo) il valore 40.

La funzione viene quindi invocata nel seguente modo:

line(80, 20, 120, 40);

Nell’immagine seguente troviamo visualizzati vari segmenti:

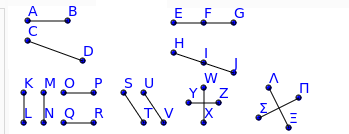
I segmenti visualizzati sono i seguenti:

• i segmenti AB e CD;
• il segmento EF che è adiacente al segmento FG;
• il segmento HI che è adiacente al segmento IJ;
• i segmenti KL e MN che sono paralleli tra loro;
• i segmenti OP e QR che sono paralleli tra loro;
• i segmenti ST e UV che sono paralleli tra loro;
• i segmenti XW e YZ che sono perpendicolari tra loro;
• i segmenti ΛΞ (lambda xi) e ΠΣ (pi sigma) che sono perpendicolari tra loro.

Disegno di figure poligonali

Un poligono è una figura geometrica piana delimitata da una linea spezzata chiusa. I segmenti che compongono la spezzata chiusa si chiamano lati del poligono. Il vertice è il punto di incontro di due lati consecutivi del poligono.

Si dicono consecutivi o adiacenti due segmenti che appartengono alla stessa retta e che hanno un solo punto in comune. Allo stesso modo, due poligoni che condividono lo stesso lato si dicono adiacenti. Anche in uno spazio a tre dimensioni, due parallelepipedi che condividono la stessa faccia si dicono adiacenti.

Nell’immagine seguente troviamo visualizzati vari segmenti:

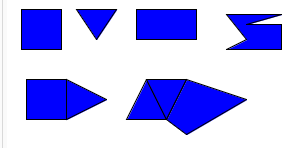
I poligoni visualizzati nell’immagine sono:

• un quadrato;
• un triangolo;
• un rettangolo;
• un poligono con sette lati;
• un quadrato adiacente ad un triangolo;
• un primo triangolo adiacente ad un secontro triangolo a sua volta adiacente ad un quadrilatero (poligono con quattro lati).

Disegno di un triangolo

Un triangolo è un poligono che ha tre lati e tre angoli. Può essere descritto da tre punti in cui originano e terminano i tre lati che lo vanno a formare.

La primitiva grafica che permette di disegnare un triangolo è triangle la cui firma è la seguente:

Syntax: triangle(x1, y1, x2, y2, x3, y3)

Parameters
    x1    Number: x-coordinate of the first point
    y1    Number: y-coordinate of the first point
    x2    Number: x-coordinate of the second point
    y2    Number: y-coordinate of the second point
    x3    Number: x-coordinate of the third point
    y3    Number: y-coordinate of the third point

I parametri formali x1 ed y1 rappresentano le coordinate del primo vertice, x2 ed y2 rappresentano le coordinate del secondo vertice, x3 ed y3 le coordinate del terzo vertice.

Per creare una triangolo i cui vertici si trovano alle coordinate (20, 60), (20, 100) e (60, 100), sostituiamo:

• al parametro formale x1 (che indica la coordinata X del primo vertice) il valore 20;
• al parametro formale y1 (che indica la coordinata Y del primo vertice) il valore 60;
• al parametro formale x2 (che indica la coordinata X del secondo vertice) il valore 20;
• al parametro formale y2 (che indica la coordinata Y del secondo vertice) il valore 100;
• al parametro formale x3 (che indica la coordinata X del terzo vertice) il valore 60;
• al parametro formale y2 (che indica la coordinata Y del secondo vertice) il valore 100.

La funzione viene quindi invocata nel seguente modo:

triangle(20, 60, 20, 100, 60, 100);

Disegno di un quadrato

Un quadrato è un poligono regolare che ha quattro lati uguali e quattro angoli retti.

La primitiva grafica che permette di disegnare un quadrato è square la cui firma è la seguente:

Syntax: square(x, y, side)

Parameters:
    x     Number: the x-coordinate of the first point
    y     Number: the y-coordinate of the first point
    side  Number: side of the square

I parametri formali x ed y sono le coordinate del punto da cui iniziare a disegnare, side è la dimensione del lato.

Per creare un quadrato con vertice in alto a sinistra nel punto (20, 140) e lato 40, sostituiamo:

• al parametro formale x (che indica la coordinata x del vertice in alto a sinistra) il valore 20;
• al parametro formale y (che indica la coordinata y del vertice in alto a sinistra) il valore 140;
• al parametro formale side (che indica il lato) il valore 40.

La funzione viene quindi invocata nel seguente modo:

square(20, 140, 40);

Disegno di un rettangolo

Il rettangolo è un poligono che ha quattro lati e quattro angoli retti. I lati opposti del rettangolo sono uguali e paralleli.

La primitiva grafica che permette di disegnare un quadrato è rect la cui firma è la seguente:

Syntax: rect(x, y, w, h)

Parameters:
    x     Number: the x-coordinate of the first point
    y     Number: the y-coordinate of the first point
    w     Number: width of the rectangle
    h     Number: height of the rectangle

I parametri formali x ed y sono le coordinate del vertice in alto a sinistra da cui iniziare a disegnare, w ed h sono le dimensioni della base e dell’altezza del rettangolo.

Per creare un rettangolo con vertice in alto a sinistra nel punto (80, 140), base 80 ed altezza 20, sostituiamo:

• al parametro formale x (che indica la coordinata x del vertice in alto a sinistra) il valore 80;
• al parametro formale y (che indica la coordinata y del vertice in alto a sinistra) il valore 140;
• al parametro formale w (che indica la base) il valore 80;
• al parametro formale h (che indica l’altezza) il valore 20.

La funzione viene quindi invocata nel seguente modo:

rect(80, 140, 80, 20);

Disegno di un generico poligono

Un poligono ha più vertici, che sono i punti di incontro di due lati del poligono. E’ possibile indicare quindi tutti i vertici di un poligono per poterlo disegnare.

La primitiva grafica che permette di disegnare un vertice in una certa posizione dell’area da disegno è vertex la cui firma (è molto simile alla firma della primitiva point) è la seguente:

Syntax: vertex(x, y)

Parameters:
    x   Number: the x-coordinate
    y   Number: the y-coordinate

I parametri formali sono x ed y e rappresentano le coordinate del vertice.

Per disegnare un poligono è quindi necessario indicare i vari vertici, invocare più volte la funzione. Ma non basta.

Per indicare che si vuole disegnare un poligono, bisogna invocare la funzione beginShape() che indica l’inizio dei vertici, poi bisogna indicare i vari vertici ed infine invocare la funzione endShape(CLOSE); per terminare il disegno del poligono, come di seguito:

beginShape();
  vertex(100, 100);
  vertex(100, 200);
  vertex(200, 100);
endShape(CLOSE);

Il parametro CLOSE della funzione endShape serve ad indicare che si vuole realizzare un poligono con una linea spezzata chiusa. Se questo parametro non viene passato alla funzione, si realizza una linea spezzata aperta, di conseguenza mancherà un lato al poligono.

Disegno di figure non poligonali

Sono dette non poligonali le figure che non sono descritte da una linea spezzata chiusa, come la circonferenza o l’ellisse.

Si dicono tangenti due oggetti geometrici che si toccano ma non si intersecano. Il punto di contatto tra curve e/o linee e/o facce della figura che si toccano senza attraversarsi è detto punto di tangenza.

Un poligono è tangente ad un’ellisse o ad una circonferenza se ha un lato toccato ma non attraversato dall’ellisse o dalla circonferenza.

Due cerchi che hanno un solo punto in comune sono tangenti.

Nell’immagine seguente troviamo visualizzati varie figure non poligonali:

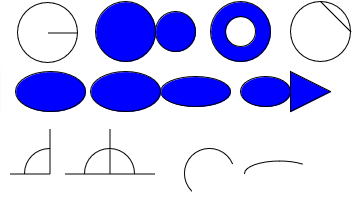
Le figure non poligonali visualizzate sono le seguenti:

• circonferenza con raggio;
• cerchi tangenti tra loro;
• corona;
• circonferenza con corda di circonferenza;
• un ellisse;
• una coppia di ellissi tangenti tra loro;
• un poligono tangente ad un ellisse;
• un angolo retto;
• un primo angolo adiacente ad un secondo angolo, formano in totale un angolo piatto;
• un arco di circonferenza;
• un arco d’ellisse.

Disegno di un cerchio

Un cerchio è una parte di piano delimitata da una circonferenza.

Una circonferenza è il luogo geometrico di punti del piano equidistanti da un punto fisso detto centro. La circonferenza è quindi una linea curva chiusa.

La distanza di qualsiasi punto della circonferenza dal centro si definisce raggio. Il diametro è il segmento che passa per il centro del cerchio e ha come estremità due punti sulla circonferenza.

L’area del piano delimitata da due circonferenze che hanno lo stesso centro è detta corona.

La primitiva grafica che permette di disegnare un cerchio è circle la cui firma è la seguente:

Syntax: circle(x, y, diameter)

Parameters:
    x           Number: x-coordinate of the centre of the circle.
    y           Number: y-coordinate of the centre of the circle.
    diameter    Number: diameter of the circle.

I parametri formali x ed y sono le coordinate del centro, diameter è la dimensione del diametro.

Per creare un cerchio con centro nel punto (100, 80) e diametro 40, sostituiamo:

• al parametro formale x (che indica la coordinata x del centro del cerchio) il valore 100;
• al parametro formale y (che indica la coordinata y del centro del cerchio) il valore 80;
• al parametro formale diameter (che indica il diametro) il valore 40.

La funzione viene quindi invocata nel seguente modo:

circle(100, 80, 40);

Disegno di un ellisse

Un ellisse è una sorta di “circonferenza schiacciata”, la si può interpretare come una sorta di “circonferenza” con larghezza ed altezza differenti. Nel caso in cui la larghezza è uguale all’altezza, la figura risultante è una vera e propria circonferenza.

Matematicamente un ellisse è il luogo geometrico dei punti del piano per i quali la somma delle distanze da due punti fissi detti “fuochi” rimane costante (a differenza la circonferenza che ha come unico fuoco il centro) .

La primitiva grafica che permette di disegnare un ellisse è ellipse, la cui firma è la seguente:

Syntax: ellipse(x, y, w, h)

Parameters:
    x     Number: the x-coordinate of the first point
    y     Number: the y-coordinate of the first point
    w     Number: width of the ellipse
    h     Number: height of the ellipse

Per creare un ellisse con vertice in alto a sinistra nel punto (60, 220), larghezza 80 ed altezza 40, sostituiamo:

• al parametro formale x (che indica la coordinata x del vertice in alto a sinistra) il valore 60;
• al parametro formale y (che indica la coordinata y del vertice in alto a sinistra) il valore 220;
• al parametro formale w (che indica la larghezza) il valore 80;
• al parametro formale h (che indica l’altezza) il valore 40.

La funzione viene quindi invocata nel seguente modo:

ellipse(60, 220, 80, 40);

Disegno di un arco di circonferenza e d’ellisse

Un arco di circonferenza è il tratto di linea curva che ha le due estremità definite da due raggi della circonferenza stessa. Un arco d’ellisse è simile ad un arco di circonferenza, con la differenza che il tratto di linea curva è parte dell’ellisse.

L’arco di circonferenza lo si realizza impostando la stessa dimensione per larghezza ed altezza della figura. L’arco d’ellisse si realizza specificando valori differenti per larghezza ed altezza della figura;

La primitiva grafica che permette di disegnare un arco di circonferenza o d’ellisse è arc la cui firma è la seguente:

Syntax: arc(x, y, w, h, start, stop, [mode])

x       Number: x-coordinate of the arc's ellipse
y       Number: y-coordinate of the arc's ellipse
w       Number: width of the arc's ellipse by default
h       Number: height of the arc's ellipse by default
start   Number: angle to start the arc, specified in radians
stop    Number: angle to stop the arc, specified in radians
mode    Constant: optional parameter to determine the way of drawing the arc. either CHORD, PIE or OPEN (Optional)

I parametri formali x ed y sono le coordinate del centro, w ed h sono le dimensioni della larghezza e dell’altezza della figura. Il parametro start indica l’angolo del primo raggio che fa da prima estremità all’arco, il parametrostop indica l’angolo del secondo raggio che fa da seconda estremità all’arco. Il parametro mode è tra parentesi quadre, quindi è opzionale, ed indica come disegnare l’arco, in particolare come collegare i due estremi d’arco.

Per creare un arco di circonferenza con centro nel punto (40, 300), con diametro 40, angolo iniziale impostato a pi greco ed angolo finale impostato a due pi greco, sostituiamo:

• al parametro formale x (che indica la coordinata x del centro) il valore 40;
• al parametro formale y (che indica la coordinata y del centro) il valore 300;
• al parametro formale w (che indica il diametro) il valore 40;
• al parametro formale h (che indica il diametro) nuovamente il valore 40;
• al parametro formale start (che indica l’angolo del primo raggio che fa da prima estremità all’arco) la costante PI (pi greco espresso in radianti);
• al parametro formale stop (indica l’angolo del secondo raggio che fa da seconda estremità all’arco) la costante TWO_PI (due pi greco espresso in radianti).

La funzione viene quindi invocata nel seguente modo:

arc(40, 300, 40, 40, PI, TWO_PI);

Per creare un arco di ellisse con centro nel punto (100, 300), con larghezza 40, altezza 80, angolo iniziale impostato a pi greco ed angolo finale impostato a due pi greco, sostituiamo:

• al parametro formale x (che indica la coordinata x del centro) il valore 100;
• al parametro formale y (che indica la coordinata y del centro) il valore 300;
• al parametro formale w (che indica la larghezza dell’ellisse) il valore 40;
• al parametro formale h (che indica l’altezza dell’ellisse) il valore 80;
• al parametro formale start (che indica l’angolo del primo raggio che fa da prima estremità all’arco) la costante PI (pi greco espresso in radianti);
• al parametro formale stop (indica l’angolo del secondo raggio che fa da seconda estremità all’arco) la costante TWO_PI (due pi greco espresso in radianti).

La funzione viene quindi invocata nel seguente modo:

arc(100, 300, 40, 80, PI, TWO_PI);

Entriamo nel dettaglio sull’uso del parametro opzionale mode, che definisce come disegnare l’arco. A questo parametro può essere assegnato il valore definito dalle seguenti costanti:

• OPEN: indica di realizzare l’arco come figura aperta, quindi senza linee di contorno per unire gli estremi. Questa è l’impostazione predefinita;
• CHORD: indica di chiudere l’arco con una linea di contorno tracciata come corda di circonferenza;
• PIE: indica di chiudere l’arco realizzato con due raggi di contorno al fine di formare un settore circolare;

Un settore circolare è l’area compresa tra l’arco di circonferenza ed i raggi che delimitano le estremità dell’arco.

Una corda di circonferenza è un segmento che ha le due estremità definite da due punti della circonferenza stessa.

Le opzioni disponibili per il parametro opzionale mode permettono di non chiudere l’arco di circonferenza, di chiuderlo con una corda di circonferenza (o di ellisse) o di chiuderlo realizzando un settore circolare, come visualizzato di seguito.

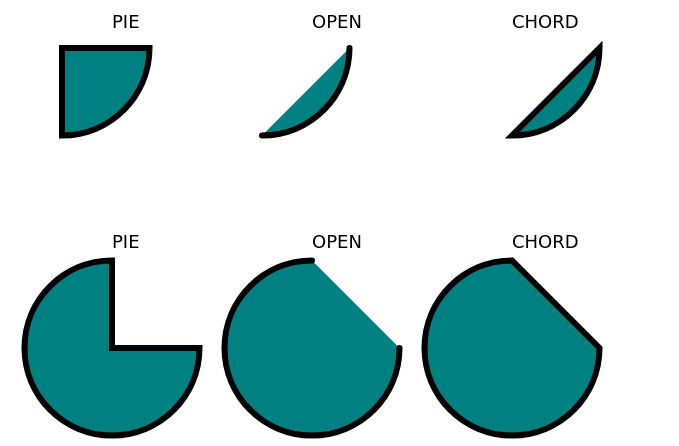
Un esempio di funzione invocata utilizzando anche il parametro mode è il seguente:

arc(100, 300, 40, 80, PI, TWO_PI, CHORD);

Disegno di un testo

Anche il disegno di un testo nell’area da disegno è considerato una primitiva grafica ed è realizzato dalla funzione text, che prevede la seguente firma:

Syntax: text(str, x, y, [x2], [y2])

Parameters
    str  String:    the alphanumeric symbols to be displayed
    x    Number:    x-coordinate of text
    y    Number:    y-coordinate of text
    x2   Number:    by default, the width of the text box (Optional)
    y2   Number:    by default, the height of the text box (Optional)

Il parametro formale str indica il testo da disegnare, i parametri formali x ed y sono le coordinate del punto in alto a sinistra dal quale disegnare il testo. I parametri formali x2 ed y2 sono tra parentesi quadre, quindi sono opzionali, e si utilizzano per indicare base ed altezza del rettangolo nel quale racchiudere il testo.

Per disegnare la frase questo è un testo partendo dal vertice in alto a sinistra nel punto (20, 340), sostituiamo:

• al parametro formale str (che indica il testo) il valore questo è un testo;
• al parametro formale x (che indica la coordinata x del vertice in alto a sinistra) il valore 20;
• al parametro formale y (che indica la coordinata y del vertice in alto a sinistra) il valore 340, quindi invochiamo la funzione nel seguente modo:

text("questo è un testo", 20, 340);

Per disegnare la frase questo è un testo partendo dal vertice in alto a sinistra nel punto (20, 360) e terminando nel vertice in basso a destra nel punto (160, 20), sostituiamo:

• al parametro formale str (che indica il testo) il valore questo è un testo;
• al parametro formale x (che indica la coordinata x del vertice in alto a sinistra) il valore 20;
• al parametro formale y (che indica la coordinata y del vertice in alto a sinistra) il valore 360;
• al parametro formale x2 (che indica la base) il valore 160 ed al parametro formale y2 (che indica l’altezza) il valore 20.

La funzione viene quindi invocata nel seguente modo:

text("questo è un testo troppo lungo", 20, 360, 160, 20);

Bisogna prestare attenzione al fatto che se il testo è troppo lungo e non può essere racchiuso nell’area del rettangolo, la parte eccessiva del testo non sarà disegnata.

Di seguito, si visualizza un esempio completo delle figure realizzate mediante il codice riportato nei vari esempi mostrati: